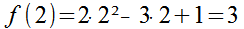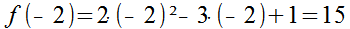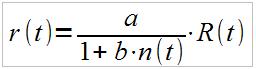New E-Book Release: Math Concepts Everyone Should Know (And Can Learn)

Well, a few weeks ago I broke my toe, which meant that I was forced to sit in my room hour after hour and think about what to do. Luckily, I found something to keep me busy: writing a new math book. The book is called Math Concepts Everyone Should Know (And Can Learn) and was completed yesterday. It is now live on Amazon (click the cover to get to the product page) for the low price of $ 2.99 and can be read without any prior knowledge in mathematics.

I must say that I’m very pleased with the result and I hope you will enjoy the learning experience. The topics are:

– Combinatorics and Probability
– Binomial Distribution
– Banzhaf Power Index
– Trigonometry
– Hypothesis Testing
– Bijective Functions And Infinity

A Formula For Risk of Nightmares

As already noted in this blog post, I recently conducted a survey on sleeping which also included the topic nightmares. The strongest effects on the occurrence of nightmares come from the variables age, depression and stress. While among younger people (age 36 or lower) roughly 50 % frequently have nightmares, the same is true for only 27 % of older people. A statistical test shows that this difference has a very strong statistical significance. Depression led the nightmare risk to rise from 24 % (no tendency for depression, self-reported) to 57 % (strong tendency for depression) and stress from 21 % (low stress level, self-reported) to 50 % (high stress level). Both increases were also statistically significant.

There were other variables that also led to an increase in the nightmare risk as well, though none of them as robust as age, depression and stress. The living conditions have a noticeable effect. A busy road increases the risk by 22 %, noisy family members or roommates by 26 % and noisy neighbors by 27 %. Also noteworthy are the effects of lifestyle. Frequently drinking stimulating beverages adds 15 % to the nightmare risk, smoking adds 16 %, alcohol adds 18 %, cannabis adds 21 % and eating late roughly 13 %. At this point, even a little before that, the differences went below the threshold for statistical significance. One more thing I can say is that the variables education, income and sleeping alone do not seem to have any effect at all on the risk of nightmares.

————————-

With all of this input I produced a predictor variable and a formula to compute the nightmare risk. Define the following variables:

Lifestyle Variable:
L = 1/5*(Stim Beverages + Smoking + Alcohol + Cannabis + Eating Late)

Circumstance Variable:
C = 1/3*(Busy Road + Noisy Family + Noisy Neighbor)

Mind Variable:
M = 1/2*(Stress + Depression)

All individual points range from 1 (no) to 5 (yes). For example, when a person never drinks stimulating beverages such as Coke or Coffee, set Stim Beverages = 1, if a person heavily consumes stimulating beverages, set Stim Beverages = 5. This way you can produce the values of L, C and M. Once these values are known for a person, one may compute the predictor P:

P = 0.6*M + 0.3*C + 0.2*L + 0.5*(90/Age)

And then insert the predictor P into this formula, that was found by regression analysis, to calculate the nightmare risk of this person:

Risk = 0.802 – 0.720 / ( 1 + (P / 4.55)^5.12 )

Where the symbol ^ means “to the power of”. To asses the accuracy of the formula, I compiled the table below. It shows the predictor range with the corresponding nightmare risk as measured in the survey and as calculated from the formula (in the bracket) for the midpoint of the predictor interval.

2.0-2.5 … 10 % (10 %)
2.5-3.0 … 19 % (13 %)
3.0-3.5 … 17 % (19 %)
3.5-4.0 … 25 % (28 %)
4.0-4.5 … 41 % (38 %)
4.5-5.0 … 45 % (48 %)
5.0-5.5 … 61 % (57 %)
5.5-6.0 … 68 % (64 %)

So while there are deviations, the formula works quite well for the most parts.

————————-

Let me demonstrate the process of finding the nightmare risk using the formula, I’ll offer myself as the test subject. Here are my values for the variables. Remember that each variable ranges from 1, a strong no, to 5, a strong yes.

Lifestyle Variable:
L = 1/5*(Stim Beverages + Smoking + Alcohol + Cannabis + Eating Late)
L = 1/5*(4 + 5 + 2 + 1 + 4) = 3.2

Circumstance Variable:
C = 1/3*(Busy Road + Noisy Family + Noisy Neighbor)
C = 1/3*(3 + 1 + 1) = 1.7

Mind Variable:
M = 1/2*(Stress + Depression)
M = 1/2*(4 + 4) = 4

Predictor:
P = 0.6*M + 0.3*C + 0.2*L + 0.5*(90/Age)
P = 0.6*4 + 0.3*1.7 + 0.2*3.2 + 0.5*(90/32) = 5

Nightmare Risk:
Risk = 0.802 – 0.720 / ( 1 + (P / 4.55)^5.12 )
Risk = 0.802 – 0.720 / ( 1 + (5 / 4.55)^5.12 ) = 0.53 = 53 %

So roughly 50/50, not that bad actually. I would say that puts me in the risk group, but luckily not the high-risk group.

What are Functions? Excerpt from “Math Dialogue: Functions”

T:

What are functions? I could just insert the standard definition here, but I fear that this might not be the best approach for those who have just started their journey into the fascinating world of mathematics. For one, any common textbook will include the definition, so if that’s all you’re looking for, you don’t need to continue reading here. Secondly, it is much more rewarding to build towards the definition step by step. This approach minimizes the risk of developing deficits and falling prey to misunderstandings.

S:

So where do we start?

T:

We have two options here. We could take the intuitive, concept-focused approach or the more abstract, mathematically rigorous path. My recommendation is to go down both roads, starting with the more intuitive approach and taking care of the strict details later on. This will allow you to get familiar with the concept of the function and apply it to solve real-world problems without first delving into sets, Cartesian products as well as relations and their properties.

S:

Sounds reasonable.

T:

Then let’s get started. For now we will think of a function as a mathematical expression that allows us to insert the value of one quantity x and spits out the value of another quantity y. So it’s basically an input-output system.

S:

Can you give me an example of this?

T:

Certainly. Here is a function: y = 2·x + 4. As you can see, there are two variables in there, the so-called independent variable x and the dependent variable y. The variable x is called independent because we are free to choose any value for it. Once a value is chosen, we do what the mathematical expression tells us to do, in this case multiply two by the value we have chosen for x and add four to that. The result of this is the corresponding value of the dependent variable y.

S:

So I can choose any value for x?

T:

That’s right, try out any value.

S:

Okay, I’ll set x = 1 then. When I insert this into the expression I get: y = 2·1 + 4 = 6. What does this tell me?

T:

This calculation tells you that the function y = 2·x + 4 links the input x = 1 with the output y = 6. Go on, try out another input.

S:

Okay, can I use x = 0?

T:

Certainly. Any real number works here.

S:

For x = 0 I get y = 2·0 + 4 = 4. So the function y = 2·x + 4 links the input x = 0 with the output y = 4.

T:

That’s right. Now it should be clear why x is called the independent variable and y the dependent variable. While you may choose any real number for x, sometimes there are common sense restrictions though, we’ll get to that later, the value of y is determined by the form of the function. A few more words on terminology and notation. Sometimes the output is also called the value of the function. We’ve just found that the function y = 2·x + 4 links the input x = 1 with the output y = 6. We could restate that as follows: at x = 1 the function takes on the value y = 6. The other input-output pair we found was x = 0 and y = 4. In other words: at x = 0 the value of the function is y = 4. Keep that in mind.

As for notation, it is very common to use f(x) instead of y. This emphasizes that the expression we are dealing with should be interpreted as a function of the independent variable x. It also allows us to note the input-output pairs in a more compact fashion by including specific values of x in the bracket. Here’s what I mean.

For the function we can write: f(x) = 2·x + 4. Inserting x = 1 we get: f(1) = 2·1 + 4 = 6 or, omitting the calculation, f(1) = 6. The latter is just a very compact way of saying that for x = 1 we get the output y = 6. In a similar manner we can write f(0) = 4 to state that at x = 0 the function takes on the value y = 4. Please insert another value for x using this notation.

S:

Will do. I’ll choose x = -1. Using this value I get: f(-1) = 2·(-1) + 4 = 2 or in short f(-1) = 2. So at x = -1 the value of the function is y = 2. Is all of this correct?

T:

Yes, that’s correct.

S:

You just mentioned that sometimes there are common sense restrictions for the independent variable x. Can I see an example of this?

T:

Okay, let’s get to this right now. Consider the function f(x) = 1/x. Please insert the value x = 1.

S:

For x = 1 I get f(1) = 1/1 = 1. So is it a problem that the output is the same as the input?

T:

Not at all, at x = 1 the function f(x) = 1/x takes on the value y = 1 and this is just fine. The input x = 2 also works well: f(2) = 1/2, so x = 2 is linked with the output y = 1/2. But we will run into problems when trying to insert x = 0.

S:

I see, division by zero. For x = 0 we have f(0) = 1/0 and this expression makes no sense.

T:

That’s right, division by zero is strictly verboten. So whenever an input x would lead to division by zero, we have to rule it out. Let’s state this a bit more elegantly. Every function has a domain. This is just the set of all inputs for which the function produces a real-valued output. For example, the domain of the function f(x) = 2·x + 4 is the set of all real numbers since we can insert any real number x without running into problems. The domain of the function f(x) = 1/x is the set of all real numbers with the number zero excluded since we can use all real numbers as inputs except for zero.

Can you see why the domain of the function f(x) = 1/(3·x – 12) is the set of all real numbers excluding the number four? If it is not obvious, try to insert x = 4.

S:

Okay, for x = 4 I get f(4) = 1/(3·4 – 12) = 1/0. Oh yes, division by zero again.

T:

Correct. That’s why we say that the domain of the function f(x) = 1/(3·x – 12) is the set of all real numbers excluding the number four. Any input x works except for x = 4. So whenever there’s an x somewhere in the denominator, watch out for this. Sometimes we have to exclude inputs for other reasons, too. Consider the function f(x) = sqrt(x). The abbreviation “sqrt” refers to the square root of x. Please compute the value of the function for the inputs x = 0, x = 1 and x = 2.

S:

Will do.

f(0) = sqrt(0) = 0

At x = 0 the value of the function is 0.

f(1) = sqrt(1) = 1

At x = 1 the value of the function is 1.

f(2) = sqrt(2) = 1.4142 …

At x = 2 the value of the function is 1.4142 … All of this looks fine to me. Or is there a problem here?

T:

No problem at all. But now try x = -1.

S:

Okay, f(-1) = sqrt(-1) = … Oh, seems like my calculator spits out an error message here. What’s going on?

T:

Seems like your calculator knows math well. There is no square root of a negative number. Think about it. We say that the square root of the number 4 is 2 because when you multiply 2 by itself you get 4. Note that 4 has another square root and for the same reason. When you multiply -2 by itself, you also get 4, so -2 is also a square root of 4.

Let’s choose another positive number, say 9. The square root of 9 is 3 because when you multiply 3 by itself you get 9. Another square root of 9 is -3 since multiplying -3 by itself leads to 9. So far so good, but what is the square root of -9? Which number can you multiply by itself to produce -9?

S:

Hmmm … 3 doesn’t work since 3 multiplied by itself is 9, -3 also doesn’t work since -3 multiplied by itself is 9. Looks like I can’t think of any number I could multiply by itself to get the result -9.

T:

That’s right, no such real number exists. In other words: there is no real-valued square root of -9. Actually, no negative number has a real-valued square root. That’s why your calculator complained when you gave him the task of finding the square root of -1. For our function f(x) = sqrt(x) all of this means that inserting an x smaller than zero would lead to a nonsensical result. We say that the domain of the function f(x) = sqrt(x) is the set of all positive real numbers including zero.

In summary, when trying to determine the domain of a function, that is, the set of all inputs that lead to a real-valued output, make sure to exclude any values of x that would a) lead to division by zero or b) produce a negative number under a square root sign. Unless faced with a particularly exotic function, the domain of the function is then simply the set of all real numbers excluding values of x that lead to division by zero and those values of x that produce negative numbers under a square root sign.

I promise we will get back to this, but I want to return to the concept of the function before doing some exercises. Let’s go back to the introductory example: f(x) = 2·x + 4. Please make an input-output table for the following inputs: x = -3, -2, -1, 0, 1, 2 and 3.

This was an excerpt from “Math Dialogue: Functions“, available on Amazon for Kindle.

What are Functions? A Short and Simple Explanation

Understanding functions is vital for anyone intending to master calculus or learning mathematical physics. For those who have never heard of the concept of the function, here’s a quick introduction. A function f(x) is a mathematical expression, you can think of it as an input-output system, establishing a connection between one independent variable x and a dependent variable y. We “throw” in a certain value of x, do what the mathematical expression f(x) demands us to do, and get a corresponding value of y in return. Here’s an example of this:

The expression on the right tells us that when given a certain value of x, we need to multiply the square of x by 2, subtract 3x from the result and in a final step add one. For example, using x = 2, the function returns the value:

So this particular function links the input x = 2 to the output y = 3. This is called the value of the function f(x) at x = 2. Of course, we are free to choose any other value for x and see what the function does with it. Inserting x = 1, we get:

So given the input x = 1, the function produces the output y = 0. Whenever this happens, a value of zero is returned, we call the respective value of x a root of the function. So the above function has one root at x = 1. Let’s check a few more values:

The first line tells us that for x = 0, the value of the function lies on y = 1. For x = -1 we get y = 6 and for x = -2 the result y = 15. What to do with this? For one, we can interpret these values geometrically. We can consider any pair of x and y as a point P(x / y) in the Cartesian coordinate system. Since we could check every x we desire and calculate the corresponding value of y using the function, the function defines a graph in the coordinate system. The graph of the above function f(x) will go through the points P(2 / 3), P(1 / 0), P(0 / 1), P(-1, 6) and P(-2 / 15). Here’s the plot:

Graph of f(x) = 2x² – 3x + 1

You can confirm that the points indeed lie on the graph by following the x-axis, as usual the horizontal axis, and determining what distance the curve has from the x-axis at a certain value of x. For example, to find the point P(2 / 3), we move, starting from the origin, two units to the right along the x-axis and then three units upwards, in direction of the y-axis. Here we meet the curve, confirming that the graph includes the point P(2 / 3). Make sure to check this for all other points we calculated. Of course, to produce such a neat plot, we need to insert a lot more than just six values for x. This uncreative work is best done by a computer. Feel free to check out the easy-to-use website graphsketch.com for this, it doesn’t cost a thing and requires no registration. Note that the plot also shows a second root at x = 0.5, the point P(0.5 / 0). Let’s make sure that this value of x is a root of our function f(x) by inserting x = 0.5 and hoping that it produces the output y = 0:

As expected. This was all very mathematical, but what practical uses are there for functions? We can use them to establish a connection between the value of one physical quantity and another. For example, through experiments or theoretical considerations we can determine a function f(p) that links the air pressure p to the air density D. It would allow us to insert any value for the air pressure p and calculate the corresponding value for the air density D, which can be quite useful. Or consider a function f(v) that establishes a connection between the velocity v of an object and the frictional forces F it experiences. This is extremely helpful when trying to determine the trajectory of the object, yet another function f(t) that specifies the link between the elapsed time t and the position x of the object. Just to give you one example of this, the function:

connects the elapsed time t (in seconds) with the corresponding height h (in meters) for an object that is dropped from a 22 m tall tower. According to this function, the object will have reached the following height after t = 1 s:

Insert any value for t and the function produces the object’s location at that time. In this case we are particularly interested in the root. For which value of the independent variable t does the function return the value zero? In other words: after what time does the object reach the ground? We could try inserting several values for t and hope that we find the right one. A more promising approach is setting up the equation f(x) = 0 and solving for x. This requires some knowledge in algebra.

Subtracting 22 on both sides leads to:

Divide by -4.91:

And apply the square root:

For this value of t the function f(t) becomes zero (due to inevitable rounding errors, not perfectly though). The rounding errors are also why I switched from the “is equal to”-sign = to the “is approximately equal to”-sign ≈. You should do the same in calculations whenever rounding a value.

Graph of f(t) = -4.91t² + 22

As you can see, functions are indeed quite useful. If you had trouble understanding the algebra that led to the root t = 2.12, consider reading my free e-book “Algebra – The Very Basics” before continuing with functions.

This was an excerpt from my e-book Math Shorts – Exponential and Trigonometric Functions

New Kindle Release: Math Shorts – Exponential and Trigonometric Functions

I’m on a roll here … another math book, comin’ right up … I’m happy to announce that today I’m expanding my “Math Shorts” series with the latest release “Math Shorts – Exponential and Trigonometric Functions”. This time it’s pre-calculus and thus serves as a bridge between my permanently free e-books “Algebra – The Very Basics” and “Math Shorts – Derivatives”. Without further ado, here’s the blurb and table of contents (click cover to get to the product page on Amazon):

Blurb:

Before delving into the exciting fields of calculus and mathematical physics, it is necessary to gain an in-depth understanding of functions. In this book you will get to know two of the most fundamental function classes intimately: the exponential and trigonometric functions. You will learn how to visualize the graph from the equation, how to set up the function from conditions for real-world applications, how to find the roots, and much more. While prior knowledge in linear and quadratic functions is helpful, it is not necessary for understanding the contents of the book as all the core concepts are developed during the discussion and demonstrated using plenty of examples. The book also contains problems along with detailed solutions to each section. So except for the very basics of algebra, no prior knowledge is required.

Once done, you can continue your journey into mathematics, from the basics all the way to differential equations, by following the “Math Shorts” series, with the recommended reading being “Math Shorts – Derivatives” upon completion of this book. From the author of “Great Formulas Explained” and “Statistical Snacks”, here’s another down-to-earth guide to the joys of mathematics.

Table of contents:

1. Exponential Functions
1.1. Definition
1.2. Exercises
1.3. Basics Continued
1.4. Exercises
1.5. A More General Form
1.6. Exercises

2. Trigonometric Functions
2.1. The Sine Function
2.2. Exercises
2.3. The Cosine Function
2.4. Exercises
2.5. Roots
2.6. Exercises
2.7. Sine Squared And More
2.8. The Tangent Function
2.9. Exercises

3. Solutions to the Problems

Have fun reading!

The Weirdness of Empty Space – Casimir Force

(This is an excerpt from The Book of Forces – enjoy!)

The forces we have discussed so far are well-understood by the scientific community and are commonly featured in introductory as well as advanced physics books. In this section we will turn to a more exotic and mysterious interaction: the Casimir force. After a series of complex quantum mechanical calculations, the Dutch physicist Hendrick Casimir predicted its existence in 1948. However, detecting the interaction proved to be an enormous challenge as this required sensors capable picking up forces in the order of 10^(-15) N and smaller. It wasn’t until 1996 that this technology became available and the existence of the Casimir force was experimentally confirmed.

So what does the Casimir force do? When you place an uncharged, conducting plate at a small distance to an identical plate, the Casimir force will pull them towards each other. The term “conductive” refers to the ability of a material to conduct electricity. For the force it plays no role though whether the plates are actually transporting electricity in a given moment or not, what counts is their ability to do so.

The existence of the force can only be explained via quantum theory. Classical physics considers the vacuum to be empty – no particles, no waves, no forces, just absolute nothingness. However, with the rise of quantum mechanics, scientists realized that this is just a crude approximation of reality. The vacuum is actually filled with an ocean of so-called virtual particles (don’t let the name fool you, they are real). These particles are constantly produced in pairs and annihilate after a very short period of time. Each particle carries a certain amount of energy that depends on its wavelength: the lower the wavelength, the higher the energy of the particle. In theory, there’s no upper limit for the energy such a particle can have when spontaneously coming into existence.

So how does this relate to the Casimir force? The two conducting plates define a boundary in space. They separate the space of finite extension between the plates from the (for all practical purposes) infinite space outside them. Only particles with wavelengths that are a multiple of the distance between the plates fit in the finite space, meaning that the particle density (and thus energy density) in the space between the plates is smaller than the energy density in the pure vacuum surrounding them. This imbalance in energy density gives rise to the Casimir force. In informal terms, the Casimir force is the push of the energy-rich vacuum on the energy-deficient space between the plates.

(Illustration of Casimir force)

It gets even more puzzling though. The nature of the Casimir force depends on the geometry of the plates. If you replace the flat plates by hemispherical shells, the Casimir force suddenly becomes repulsive, meaning that this specific geometry somehow manages to increase the energy density of the enclosed vacuum. Now the even more energy-rich finite space pushes on the surrounding infinite vacuum. Trippy, huh? So which shapes lead to attraction and which lead to repulsion? Unfortunately, there is no intuitive way to decide. Only abstract mathematical calculations and sophisticated experiments can provide an answer.

We can use the following formula to calculate the magnitude of the attractive Casimir force FCS between two flat plates. Its value depends solely on the distance d (in m) between the plates and the area A (in m²) of one plate. The letters h = 6.63·10^(-34) m² kg/s and c = 3.00·10^8 m/s represent Plank’s constant and the speed of light.

FCS = π·h·c·A / (480·d^4) ≈ 1.3·10^(-27)·A / d^4

(The sign ^ stands for “to the power”) Note that because of the exponent, the strength of the force goes down very rapidly with increasing distance. If you double the size of the gap between the plates, the magnitude of the force reduces to 1/2^4 = 1/16 of its original value. And if you triple the distance, it goes down to 1/3^4 = 1/81 of its original value. This strong dependence on distance and the presence of Plank’s constant as a factor cause the Casimir force to be extremely weak in most real-world situations.

————————————-

Example 24:

a) Calculate the magnitude of the Casimir force experienced by two conducting plates having an area A = 1 m² each and distance d = 0.001 m (one millimeter). Compare this to their mutual gravitational attraction given the mass m = 5 kg of one plate.

b) How close do the plates need to be for the Casimir force to be in the order of unity? Set FCS = 1 N.

Solution:

a)

Inserting the given values into the formula for the Casimir force leads to (units not included):

FCS = 1.3·10^(-27)·A/d^4
FCS = 1.3·10^(-27) · 1 / 0.0014
FCS ≈ 1.3·10^(-15) N

Their gravitational attraction is:

FG = G·m·M / r²
FG = 6.67·10^(-11)·5·5 / 0.001²
FG ≈ 0.0017 N

This is more than a trillion times the magnitude of the Casimir force – no wonder this exotic force went undetected for so long.  I should mention though that the gravitational force calculated above should only be regarded as a rough approximation as Newton’s law of gravitation is tailored to two attracting spheres, not two attracting plates.

b)

Setting up an equation we get:

FCS = 1.3·10^(-27)·A/d^4
1 = 1.3·10^(-27) · 1 / d^4

Multiply by d4:

d4 = 1.3·10^(-27)

And apply the fourth root:

d ≈ 2·10^(-7) m = 200 nanometers

This is roughly the size of a common virus and just a bit longer than the wavelength of violet light.

————————————-

The existence of the Casimir force provides an impressive proof that the abstract mathematics of quantum mechanics is able to accurately describe the workings of the small-scale universe. However, many open questions remain. Quantum theory predicts the energy density of the vacuum to be infinitely large. According to Einstein’s theory of gravitation, such a concentration of energy would produce an infinite space-time curvature and if this were the case, we wouldn’t exist. So either we don’t exist (which I’m pretty sure is not the case) or the most powerful theories in physics are at odds when it comes to the vacuum.

The Best Math-Related Memes

(Explanation to the image above: the square root of minus one is the imaginary unit, usually abbreviated by i, 2 to the power of 3 is 8, the third symbol is the summation sign, the last one of course is pi … so it reads: “i 8 sum pi” = “I ate some pie”)

New Release for Kindle: Antimatter Propulsion

I’m very excited to announce the release of my latest ebook called “Antimatter Propulsion”. I’ve been working working on it like a madman for the past few months, going through scientific papers and wrestling with the jargon and equations. But I’m quite satisfied with the result. Here’s the blurb, the table of contents and the link to the product page. No prior knowledge is required to enjoy the book.

Many popular science fiction movies and novels feature antimatter propulsion systems, from the classic Star Trek series all the way to Cameron’s hit movie Avatar. But what exactly is antimatter? And how can it be used accelerate rockets? This book is a gentle introduction to the science behind antimatter propulsion. The first section deals with antimatter in general, detailing its discovery, behavior, production and storage. This is followed by an introduction to propulsion, including a look at the most important quantities involved and the propulsion systems in use or in development today. Finally, the most promising antimatter propulsion and rocket concepts are presented and their feasibility discussed, from the solid core concept to antimatter initiated microfusion engines, from the Valkyrie project to Penn State’s AIMStar spacecraft.

Section 1: Antimatter

The Atom
Dirac’s Idea
Anti-Everything
An Explosive Mix
Proton and Anti-Proton Annihilation
Sources of Antimatter
Storing Antimatter
Getting the Fuel

Section 2: Propulsion Basics

Conservation of Momentum
♪ Throw, Throw, Throw Your Boat ♫
So What’s The Deal?
May The Thrust Be With You
Acceleration
Specific Impulse and Fuel Requirements
Chemical Propulsion
Electric Propulsion
Fusion Propulsion

Section 3: Antimatter Propulsion Concepts

Solid Core Concept
Plasma Core Concept
Beamed Core Concept
Antimatter Catalyzed Micro-Fission / Fusion
Antimatter Initiated Micro-Fusion

Section 4: Antimatter Rocket Concepts

Project Valkyrie
ICAN-II
AIMStar
Dust Shields

You can purchase “Antimatter Propulsion” here for $ 2.99.

New Release for Kindle: Math Shorts – Derivatives

The rich and exciting field of calculus begins with the study of derivatives. This book is a practical introduction to derivatives, filled with down-to-earth explanations, detailed examples and lots of exercises (solutions included). It takes you from the basic functions all the way to advanced differentiation rules and proofs. Check out the sample for the table of contents and a taste of the action. From the author of “Mathematical Shenanigans”, “Great Formulas Explained” and the “Math Shorts” series. A supplement to this book is available under the title “Exercises to Math Shorts – Derivatives”. It contains an additional 28 exercises including detailed solutions.

Note: Except for the very basics of algebra, no prior knowledge is required to enjoy this book.

Table of Contents:

– Section 1: The Big Picture

– Section 2: Basic Functions and Rules

Power Functions
Sum Rule and Polynomial Functions
Exponential Functions
Logarithmic Functions
Trigonometric Functions

– Section 3: Advanced Differentiation Rules

I Know That I Know Nothing
Product Rule
Quotient Rule
Chain Rule

– Section 4: Limit Definition and Proofs

The Formula
Power Functions
Constant Factor Rule and Sum Rule
Product Rule

– Section 5: Appendix

Solutions to the Problems
Copyright and Disclaimer
Request to the Reader

Differential Equations – The Big Picture

Population Growth

So you want to learn about differential equations? Excellent choice. Differential equations are not only of central importance to science, they can also be quite stimulating and fun (that’s right). In the broadest sense, a differential equation is any equation that connects a function with one or more of its derivatives. What makes these kinds of equations particularly important?

Remember that a derivative expresses the rate of change of a quantity. So the differential equation basically establishes a link between the rate of change of said quantity and its current value. Such a link is very common in nature. Consider population growth. It is obvious that the rate of change will depend on the current size of the population. The more animals there are, the more births (and deaths) we can expect and hence the faster the size of the population will change.

A commonly used model for population growth is the exponential model. It is based on the assumption that the rate of change is proportional to the current size of the population. Let’s put this into mathematical form. We will denote the size of the population by N (measured in number of animals) and the first derivative with respect to time by dN/dt (measured in number of animals per unit time). Note that other symbols often used for the first derivative are N’ and Ṅ. We will however stick to the so-called Leibniz notation dN/dt as it will prove to be quite instructive when dealing with separable differential equations. That said, let’s go back to the exponential model.

With N being the size of the population and dN/dt the corresponding rate of change, our assumption of proportionality between the two looks like this:

with r being a constant. We can interpret r as the growth rate. If r > 0, then the population will grow, if r < 0, it will shrink. This model has proven to be successful for relatively small animal populations. However, there’s one big flaw: there is no limiting value. According to the model, the population would just keep on growing and growing until it consumes the entire universe. Obviously and luckily, bacteria in Petri dish don’t behave this way. For a more accurate model, we need to take into account the limits of the environment.

The differential equation that forms the basis of the logistic model, called Verhulst equation in honor of the Belgian mathematician Pierre François Verhulst, does just that. Just like the differential equation for exponential growth, it relates the current size N of the population to its rate of change dN/dt, but also takes into account the finite capacity K of the environment:

Take a careful look at the equation. Even without any calculations a differential equation can tell a vivid story. Suppose for example that the population is very small. In this case N is much smaller than K, so the ratio N/K is close to zero. This means that we are back to the exponential model. Hence, the logistic model contains the exponential model as a special case. Great! The other extreme is N = K, that is, when the size of the population reaches the capacity. In this case the ratio N/K is one and the rate of change dN/dt becomes zero, which is exactly what we were expecting. No more growth at the capacity.

Definition and Equation of Motion

Now that you have seen two examples of differential equations, let’s generalize the whole thing. For starters, note that we can rewrite the two equations as such:

Denoting the dependent variable with x (instead of N) and higher order derivatives with dnx/dtn (with n = 2 resulting in the second derivative, n = 3 in the third derivative, and so on), the general form of a differential equation looks like this:

Wow, that looks horrible! But don’t worry. We just stated in the broadest way possible that a differential equation is any equation that connects a function x(t) with one or more its derivatives dx/dt, d2x/dt2, and so on. The above differential equation is said to have the order n. Up to now, we’ve only been dealing with first order differential equations.

The following equation is an example of a second order differential equation that you’ll frequently come across in physics. Its solution x(t) describes the position or angle over time of an oscillating object (spring, pendulum).

with c being a constant. Second order differential equations often arise naturally from Newton’s equation of motion. This law, which even the most ruthless crook will never be able to break, states that the object’s mass m times the acceleration a experienced by it is equal to the applied net force F:

The force can be a function of the object’s location x (spring), the velocity v = dx/dt (air resistance), the acceleration a = d2x/dt2 (Bremsstrahlung) and time t (motor):

Hence the equation of motion becomes:

A second order differential equation which leads to the object’s position over time x(t) given the forces involved in shaping its motion. It might not look pretty to some (it does to me), but there’s no doubt that it is extremely powerful and useful.

Equilibrium Points

To demonstrate what equilibrium points are and how to compute them, let’s take the logistic model a step further. In the absence of predators, we can assume the fish in a certain lake to grow according to Verhulst’s equation. The presence of fishermen obviously changes the dynamics of the population. Every time a fisherman goes out, he will remove some of the fish from the population. It is safe to assume that the success of the fisherman depends on the current size of the population: the more fish there are, the more he will be able to catch. We can set up a modified version of Verhulst’s equation to describe the situation mathematically:

with a constant c > 0 that depends on the total number of fishermen, the frequency and duration of their fishing trips, the size of their nets, and so on. Solving this differential equation is quite difficult. However, what we can do with relative ease is finding equilibrium points.

Remember that dN/dt describes the rate of change of the population. Hence, by setting dN/dt = 0, we can find out if and when the population reaches a constant size. Let’s do this for the above equation.

This leads to two solutions:

The first equilibrium point is quite boring. Once the population reaches zero, it will remain there. You don’t need to do math to see that. However, the second equilibrium point is much more interesting. It tells us how to calculate the size of the population in the long run from the constants. We can also see that a stable population is only possible if c < r.

Note that not all equilibrium points that we find during such an analysis are actually stable (in the sense that the system will return to the equilibrium point after a small disturbance). The easiest way to find out whether an equilibrium point is stable or not is to plot the rate of change, in this case dN/dt, over the dependent variable, in this case N. If the curve goes from positive to negative values at the equilibrium point, the equilibrium is stable, otherwise it is unstable.

(This was an excerpt from my e-book “Math Shorts – Introduction to Differential Equations”)

Modeling Theme Park Queues

Who doesn’t love a day at the theme park? You can go on thrilling roller‒coaster rides, enjoy elaborate shows, have a tasty lunch in between or just relax and take in the scenery. Of course there’s one thing that does spoil the fun a bit: the waiting. For the most popular attractions waiting times of around one hour are not uncommon during peak times, while the ride itself may be over in no more than two or three minutes.

Let’s work towards a basic model for queues in theme parks and other situations in which queues commonly arise. We will assume that the passing rate R(t), that is, the number of people passing the entrance of the attraction per unit time, is given. How many of these will enter the line? This will depend on the popularity of the attraction as well as the current size of the line. The more people are already in the line, the less likely others are to join. We’ll denote the number of people in the line at time t with n(t) and use this ansatz for the rate r(t) at which people join the queue:

The constant a expresses the popularity of the attraction (more specifically, it is the percentage of passers‒by that will use the attraction if no queue is present) and the constant b is a “line repulsion” factor. The stronger visitors are put off by the presence of a line, the higher its value will be. How does the size of the line develop over time given the above function? We assume that the maximum serving rate is c people per unit time. So the rate of change for the number of people in line is (for n(t) ≥ 0):

In case the numerical evaluation returns a value n(t) < 0 (which is obviously nonsense, but a mathematical possibility given our ansatz), we will force n(t) = 0. An interesting variation, into which we will not dive much further though, is to include a time lag. Usually the expected waiting time is displayed to visitors on a screen. The visitors make their decision on joining the line based on this information. However, the displayed waiting time is not updated in real‒time. We have to expect that there’s a certain delay d between actual and displayed length of the line. With this effect included, our equation becomes:

Simulation

For the numerical solution we will go back to the delay‒free version. We choose one minute as our unit of time. For the passing rate, that is, the people passing by per minute, we set:

R(t) = 0.00046 · t · (720 ‒ t)

We can interpret this function as such: at t = 0 the park opens and the passing rate is zero. It then grows to a maximum of 60 people per minute at t = 360 minutes (or 6 hours) and declines again. At t = 720 minutes (or 12 hours) the park closes and the passing rate is back to zero. We will assume the popularity of the attraction to be:

a = 0.2

So if there’s no line, 20 % of all passers‒by will make use of the attraction. We set the maximum service rate to:

c = 5 people per minute

What about the “line repulsion” factor? Let’s assume that if the line grows to 200 people (given the above service rate this would translate into a waiting time of 40 minutes), the willingness to join the line drops from the initial 20 % to 10 %.

→ b = 0.005

Given all these inputs and the model equation, here’s how the queue develops over time:

It shows that no line will form until around t = 100 minutes into opening the park (at which point the passing rate reaches 29 people per minute). Then the queue size increases roughly linearly for the next several hours until it reaches its maximum value of n = 256 people (waiting time: 51 minutes) at t = 440 minutes. Note that the maximum value of the queue size occurs much later than the maximum value of the passing rate. After reaching a maximum, there’s a sharp decrease in line length until the line ceases to be at around t = 685 minutes. Further simulations show that if you include a delay, there’s no noticeable change as long as the delay is in the order of a few minutes.

(This was an excerpt from my ebook “Mathematical Shenanigans”)

New Release for Kindle: Math Shorts – Integrals

Yesterday I released the second part of my “Math Shorts” series. This time it’s all about integrals. Integrals are among the most useful and fascinating mathematical concepts ever conceived. The ebook is a practical introduction for all those who don’t want to miss out. In it you’ll find down-to-earth explanations, detailed examples and interesting applications. Check out the sample (see link to product page) a taste of the action.

Important note: to enjoy the book, you need solid prior knowledge in algebra and calculus. This means in particular being able to solve all kinds of equations, finding and interpreting derivatives as well as understanding the notation associated with these topics.

Click the cover to open the product page:

Here’s the TOC:

Section 1: The Big Picture
-Anti-Derivatives
-Integrals
-Applications

Section 2: Basic Anti-Derivatives and Integrals
-Power Functions
-Sums of Functions
-Examples of Definite Integrals
-Exponential Functions
-Trigonometric Functions
-Putting it all Together

Section 3: Applications
-Area – Basics
-Area – Numerical Example
-Area – Parabolic Gate
-Area – To Infinity and Beyond
-Volume – Basics
-Volume – Numerical Example
-Volume – Gabriel’s Horn
-Average Value
-Kinematics

Section 4: Advanced Integration Techniques
-Substitution – Basics
-Substitution – Indefinite Integrals
-Substitution – Definite Integrals
-Integration by Parts – Basics
-Integration by Parts – Indefinite Integrals
-Integration by Parts – Definite Integrals

Section 5: Appendix
-Formulas To Know By Heart
-Greek Alphabet
-Copyright and Disclaimer
-Request to the Reader

Enjoy!

New Release for Kindle: Introduction to Differential Equations

Differential equations are an important and fascinating part of mathematics with numerous applications in almost all fields of science. This book is a gentle introduction to the rich world of differential equations filled with no-nonsense explanations, step-by-step calculations and application-focused examples.

Important note: to enjoy the book, you need solid prior knowledge in algebra and calculus. This means in particular being able to solve all kinds of equations, finding and interpreting derivatives, evaluating integrals as well as understanding the notation that goes along with those.

Click the cover to open the product page:

Here’s the TOC:

Section 1: The Big Picture

-Population Growth
-Definition and Equation of Motion
-Equilibrium Points
-Some More Terminology

Section 2: Separable Differential Equations

-Approach
-Exponential Growth Revisited
-Fluid Friction
-Logistic Growth Revisited

Section 3: First Order Linear Differential Equations

-Approach
-More Fluid Friction
-Heating and Cooling
-Pure, Uncut Mathematics
-Bernoulli Differential Equations

Section 4: Second Order Homogeneous Linear Differential Equations (with Constant Coefficients)

-Wait, what?
-Oscillating Spring
-Numerical Example
-The Next Step – Non-Homogeneous Equations

Section 5: Appendix

-Formulas To Know By Heart
-Greek Alphabet
-Copyright and Disclaimer
-Request to the Reader

Note: With this book release I’m starting my “Math Shorts” Series. The next installment “Math Shorts – Integrals” will be available in just a few days! (Yes, I’m working like a mad man on it)

Motion With Constant Acceleration (Examples, Exercises, Solutions)

An abstraction often used in physics is motion with constant acceleration. This is a good approximation for many different situations: free fall over small distances or in low-density atmospheres, full braking in car traffic, an object sliding down an inclined plane, etc … The mathematics behind this special case is relatively simple. Assume the object that is subject to the constant acceleration a (in m/s²) initially has a velocity v(0) (in m/s). Since the velocity is the integral of the acceleration function, the object’s velocity after time t (in s) is simply:

1) v(t) = v(0) + a · t

For example, if a car initially goes v(0) = 20 m/s and brakes with a constant a = -10 m/s², which is a realistic value for asphalt, its velocity after a time t is:

v(t) = 20 – 10 · t

After t = 1 second, the car’s speed has decreased to v(1) = 20 – 10 · 1 = 10 m/s and after t = 2 seconds the car has come to a halt: v(2) = 20 – 10 · 2 = 0 m/s. As you can see, it’s all pretty straight-forward. Note that the negative acceleration (also called deceleration) has led the velocity to decrease over time. In a similar manner, a positive acceleration will cause the speed to go up. You can read more on acceleration in this blog post.

What about the distance x (in m) the object covers? We have to integrate the velocity function to find the appropriate formula. The covered distance after time t is:

2) x(t) = v(0) · t + 0.5 · a · t²

While that looks a lot more complicated, it is really just as straight-forward. Let’s go back to the car that initially has a speed of v(0) = 20 m/s and brakes with a constant a = -10 m/s². In this case the above formula becomes:

x(t) = 20 · t – 0.5 · 10 · t²

After t = 1 second, the car has traveled x(1) = 20 · 1 – 0.5 · 10 · 1² = 15 meters. By the time it comes to a halt at t = 2 seconds, it moved x(2) = 20 · 2 – 0.5 · 10 · 2² = 20 meters. Note that we don’t have to use the time as a variable. There’s a way to eliminate it. We could solve equation 1) for t and insert the resulting expression into equation 2). This leads to a formula connecting the velocity v and distance x.

3)

Solved for x it looks like this:

3)’

It’s a very useful formula that you should keep in mind. Suppose a tram accelerates at a constant a = 1.3 m/s², which is also a realistic value, from rest (v(0) = 0 m/s). What distance does it need to go to full speed v = 10 m/s? Using equation 3)’ we can easily calculate this:

————————————————————————————-

Here are a few exercises and solutions using the equations 1), 2) and 3).

1. During free fall (air resistance neglected) an object accelerates with about a = 10 m/s. Suppose the object is dropped, that is, it is initially at rest (v(0) = 0 m/s).

a) What is its speed after t = 3 seconds?
b) What distance has it traveled after t = 3 seconds?
c) Suppose we drop the object from a tower that is x = 20 meters tall. At what speed will it impact the ground?
d) How long does the drop take?

Hint: in exercise d) solve equation 1) for t and insert the result from c)

2. During the reentry of space crafts accelerations can be as high as a = -70 m/s². Suppose the space craft initially moves with v(0) = 6000 m/s.

a) What’s the speed and covered distance after t = 10 seconds?
b) How long will it take the space craft to half its initial velocity?
c) What distance will it travel during this time?

3. An investigator arrives at the scene of a car crash. From the skid marks he deduces that it took the car a distance x = 55 meters to come to a halt. Assume full braking (a = -10 m/s²). Was the car initially above the speed limit of 30 m/s?

————————————————————————————-

Solutions to the exercises:

Exercise 1

a) 30 m/s
b) 45 m
c) 20 m/s
d) 2 s

Exercise 2

a) 5,300 m/s and 56,500 m
b) 42.9 s (rounded)
c) 192,860 m (rounded)

Exercise 3

Yes (he was initially going 33.2 m/s)

————————————————————————————-

To learn the basic math you need to succeed in physics, check out the e-book “Algebra – The Very Basics”. For an informal introduction to physics, check out the e-book “Physics! In Quantities and Examples”. Both are available at low prices and exclusively for Kindle.

Mathematics of Banner Ads: Visitor Loyalty and CTR

First of all: why should a website’s visitor loyalty have any effect at all on the CTR we can expect to achieve with a banner ad? What does the one have to do with the other? To understand the connection, let’s take a look at an overly simplistic example. Suppose we place a banner ad on a website and get in total 3 impressions (granted, not a realistic number, but I’m only trying to make a point here). From previous campaigns we know that a visitor clicks on our ad with a probability of 0.1 = 10 % (which is also quite unrealistic).

The expected number of clicks from these 3 impressions is …

… 0.1 + 0.1 + 0.1 = 0.3 when all impressions come from different visitors.

… 1 – 0.9^3 = 0.27 when all impressions come from only one visitor.

(the symbol ^ stands for “to the power of”)

This demonstrates that we can expect more clicks if the website’s visitor loyalty is low, which might seem counter-intuitive at first. But the great thing about mathematics is that it cuts through bullshit better than the sharpest knife ever could. Math doesn’t lie. Let’s develop a model to show that a higher vistor loyalty translates into a lower CTR.

Suppose we got a number of I impressions on the banner ad in total. We’ll denote the percentage of visitors that contributed …

… only one impression by f(1)
… two impressions by f(2)
… three impressions by f(3)

And so on. Note that this distribution f(n) must satisfy the condition ∑[n] n·f(n) = I for it all to check out. The symbol ∑[n] stands for the sum over all n.

We’ll assume that the probability of a visitor clicking on the ad is q. The probability that this visitor clicks on the ad at least once during n visits is just: p(n) = 1 – (1 – q)^n (to understand why you have the know about the multiplication rule of statistics – if you’re not familiar with it, my ebook “Statistical Snacks” is a good place to start).

Let’s count the expected number of clicks for the I impressions. Visitors …

… contributing only one impression give rise to c(1) = p(1) + p(1) + … [f(1)·I addends in total] = p(1)·f(1)·I clicks

… contributing two impressions give rise to c(2) = p(2) + p(2) + … [f(2)·I/2 addends in total] = p(2)·f(2)·I/2 clicks

… contributing three impressions give rise to c(3) = p(3) + p(3) + … [f(3)·I/3 addends in total] = p(3)·f(3)·I/3 clicks

And so on. So the total number of clicks we can expect is: c = ∑[n] p(n)·f(n)/n·I. Since the CTR is just clicks divided by impressions, we finally get this beautiful formula:

CTR = ∑[n] p(n)·f(n)/n

The expression p(n)/n decreases as n increases. So a higher visitor loyalty (which mathematically means that f(n) has a relatively high value for n greater than one) translates into a lower CTR. One final conclusion: the formula can also tell us a bit about how the CTR develops during a campaign. If a website has no loyal visitors, the CTR will remain at a constant level, while for websites with a lot of loyal visitors, the CTR will decrease over time.

Compressors: Formula for Maximum Volume

Suppose we have an audio signal which peaks at L decibels. We apply a compressor with a threshold T (with T being smaller than L, otherwise the compressor will not spring into action) and ratio r. How does this effect the maximum volume of the audio signal? Let’s derive a formula for that. Remember that the compressor leaves the parts of the signal that are below the threshold unchanged and dampens the excess volume (threshold to signal level) by the ratio we set. So the dynamic range from the threshold to the peak, which is L – T, is compressed to (L – T) / r. Hence, the peak volume after compression is:

L’ = T + (L – T) / r

For example, suppose our mix peaks at L = – 2 dB. We compress it using a threshold of T = – 10 dB and a ratio r = 2:1. The maximum volume after compression is:

L’ = – 10 dB + ( – 2 dB – (- 10 dB) ) / 2 = – 10 dB + 8 dB / 2 = – 6 dB

Simpson’s Paradox And Gender Discrimination

One sunny day we arrive at work in the university administration to find a lot of aggressive emails in our in‒box. Just the day before, a news story about gender discrimination in academia was published in a popular local newspaper which included data from our university. The emails are a result of that. Female readers are outraged that men were accepted at the university at a higher rate, while male readers are angry that women were favored in each course the university offers. Somewhat puzzled, you take a look at the data to see what’s going on and who’s wrong.

The university only offers two courses: physics and sociology. In total, 1000 men and 1000 women applied. Here’s the breakdown:

Physics:

800 men applied ‒ 480 accepted (60 %)
100 women applied ‒ 80 accepted (80 %)

Sociology:

200 men applied ‒ 40 accepted (20 %)
900 women applied ‒ 360 accepted (40 %)

Seems like the male readers are right. In each course women were favored. But why the outrage by female readers? Maybe they focused more on the following piece of data. Let’s count how many men and women were accepted overall.

Overall:

1000 men applied ‒ 520 accepted (52 %)
1000 women applied ‒ 440 accepted (44 %)

Wait, what? How did that happen? Suddenly the situation seems reversed. What looked like a clear case of discrimination of male students turned into a case of discrimination of female students by simple addition. How can that be explained?

The paradoxical situation is caused by the different capacities of the two departments as well as the student’s overall preferences. While the physics department, the top choice of male students, could accept 560 students, the smaller sociology department, the top choice of female students, could only take on 400 students. So a higher acceptance rate of male students is to be expected even if women are slightly favored in each course.

While this might seem to you like an overly artificial example to demonstrate an obscure statistical phenomenon, I’m sure the University of California (Berkeley) would beg to differ. It was sued in 1973 for bias against women on the basis of these admission rates:

8442 men applied ‒ 3715 accepted (44 %)
4321 women applied ‒ 1512 accepted (35 %)

A further analysis of the data however showed that women were favored in almost all departments ‒ Simpson’s paradox at work. The paradox also appeared (and keeps on appearing) in clinical trials. A certain treatment might be favored in individual groups, but still prove to be inferior in the aggregate data.

Overtones – What They Are And How To Compute Them

In theory, hitting the middle C on a piano should produce a sound wave with a frequency of 523.25 Hz and nothing else. However, running the resulting audio through a spectrum analyzer, it becomes obvious that there’s much more going on. This is true for all other instruments, from tubas to trumpets, basoons to flutes, contrabasses to violins. Play any note and you’ll get a package of sound waves at different frequencies rather than just one.

First of all: why is that? Let’s focus on stringed instruments. When you plug the string, it goes into its most basic vibration mode: it moves up and down as a whole at a certain frequency f. This is the so called first harmonic (or fundamental). But shortly after that, the nature of the vibration changes and the string enters a second mode: while one half of the string moves up, the other half moves down. This happens naturally and is just part of the string’s dynamics. In this mode, called the second harmonic, the vibration accelerates to a frequency of 2 * f. The story continues in this fashion as other modes of vibration appear: the third harmonic at a frequency 3 * f, the fourth harmonic at 4 * f, and so on.

A note is determined by the frequency. As already stated, the middle C on the piano should produce a sound wave with a frequency of 523.25 Hz. And indeed it does produce said sound wave, but it is only the first harmonic. As the string continues to vibrate, all the other harmonics follow, producing overtones. In the picture below you can see which notes you’ll get when playing a C (overtone series):

(The marked notes are only approximates. Taken from http://legacy.earlham.edu)

Quite the package! And note that the major chord is fully included within the first four overtones. So it’s buy a note, get a chord free. And unless you digitally produce a note, there’s no avoiding it. You might wonder why it is that we don’t seem to perceive the additional notes. Well, we do and we don’t. We don’t perceive the overtones consciously because the amplitude, and thus volume, of each harmonic is smaller then the amplitude of the previous one (however, this is a rule of thumb and exceptions are possible, any instrument will emphasize some overtones in particular). But I can assure you that when listening to a digitally produced note, you’ll feel that something’s missing. It will sound bland and cold. So unconsciously, we do perceive and desire the overtones.

If you’re not interested in mathematics, feel free to stop reading now (I hope you enjoyed the post so far). For all others: let’s get down to some mathematical business. The frequency of a note, or rather of its first harmonic, can be computed via:

(1) f(n) = 440 * 2^n/12

With n = 0 being the chamber pitch and each step of n one half-tone. For example, from the chamber pitch (note A) to the middle C there are n = 3 half-tone steps (A#, B, C). So the frequency of the middle C is:

f(3) = 440 * 2^3/12 = 523.25 Hz

As expected. Given a fundamental frequency f = F, corresponding to a half-step-value of n = N, the freqency of the k-th harmonic is just:

(2) f(k) = k * F = k * 440 * 2^N/12

Equating (1) and (2), we get a relationship that enables us to identify the musical pitch of any overtone:

440 * 2^n/12 = k * 440 * 2^N/12

2^n/12 = k * 2^N/12

n/12 * ln(2) = ln(k) + N/12 * ln(2)

n/12 = ln(k)/ln(2) + N/12

(3) n – N = 12 * ln(k) / ln(2) ≈ 17.31 * ln(k)

The equation results in this table:

k	n – N (rounded)
1	0
2	12
3	19
4	24
5	28

And so on. How does this tell us where the overtones are? Read it like this:

• The first harmonic (k = 1) is zero half-steps from the fundamental (n-N = 0). So far, so duh.

• The second harmonic (k = 2) is twelve half-steps, or one octave, from the fundamental (n-N = 12).

• The third harmonic (k = 3) is nineteen half-steps, or one octave and a quint, from the fundamental (n-N = 19).

• The fourth harmonic (k = 4) is twenty-four half-steps, or two octaves, from the fundamental (n-N = 24).

• The fifth harmonic (k = 5) is twenty-wight half-steps, or two octaves and a third, from the fundamental (n-N = 28).

So indeed the formula produces the correct overtone series for any note. And for any note the same is true: The second overtone is exactly one octave higher, the third harmonic one octave and a quint higher, and so on. The corresponding major chord is always contained within the first five harmonics.

The Doppler Effect in Pictures

The siren of an approaching police car will sound at a higher pitch, the light of an approaching star will be shifted towards blue and a passing supersonic jet will create a violent thunder. What do these phenomenon have in common? All of them are a result of the Doppler effect. To understand how it arises, just take a look at the animations below.

Stationary Source: The waves coming from the source propagate symmetrically.

Subsonic Source (moving below sound speed): Compression of waves in direction of motion.

Sonic Source (moving at sound speed): Maximum compression.

Supersonic Source (moving beyond sound speed): Source overtakes its waves, formation of Mach cone and sonic boom.

(Pictures taken from http://www.acs.psu.edu)

A Brief Look At Car-Following Models

Recently I posted a short introduction to recurrence relations – what they are and how they can be used for mathematical modeling. This post expands on the topic as car-following models are a nice example of recurrence relations applied to the real-world.

Suppose a car is traveling on the road at the speed u(t) at time t. Another car approaches this car from behind and starts following it. Obviously the driver of the car that is following cannot choose his speed freely. Rather, his speed v(t) at time t will be a result of whatever the driver in the leading car is doing.

The most basic car-following model assumes that the acceleration a(t) at time t of the follower is determined by the difference in speeds. If the leader is faster than the follower, the follower accelerates. If the leader is slower than the follower, the follower decelerates. The follower assumes a constant speed if there’s no speed difference. In mathematical form, this statement looks like this:

a(t) = λ * (u(t) – v(t))

The factor λ (sensitivity) determines how strongly the follower accelerates in response to a speed difference. To be more specific: it is the acceleration that results from a speed difference of one unit.

——————————————

Before we go on: how is this a recurrence relation? In a recurrence relation we determine a quantity from its values at an earlier time. This seems to be missing here. But remember that the acceleration is given by:

a(t) = (v(t+h) – v(t)) / h

with h being a time span. Inserted into the above car-following equation, we can see that it indeed implies a recurrence relation.

——————————————

Our model is still very crude. Here’s the biggest problem: The response of the driver is instantaneous. He picks up the speed difference at time t and turns this information into an acceleration also at time t. But more realistically, there will be a time lag. His response at time t will be a result of the speed difference at an earlier time t – Λ, with Λ being the reaction time.

a(t) = λ * (u(t – Λ) – v(t – Λ))

The reaction time is usually in the order of one second and consist of the time needed to process the information as well as the time it takes to move the muscles and press the pedal. There are several things we can do to make the model even more realistic. First of all, studies show that the speed difference is not the only factor. The distance d(t) between the leader and follower also plays an important role. The smaller it is, the stronger the follower will react. We can take this into account by putting the distance in the denominator:

a(t) = (λ / d(t)) * (u(t – Λ) – v(t – Λ))

You can also interpret this as making the sensitivity distance-dependent. There’s still one adjustment we need to make. The above model allows any value of acceleration, but we know that we can only reach certain maximum values in a car. Let’s symbolize the maximum acceleration by a(acc) and the maximum deceleration by a(dec). The latter will be a number smaller than zero since deceleration is by definition negative acceleration. We can write:

a(t) = a(acc) if (λ / d(t)) * (u(t – Λ) – v(t – Λ)) > a(acc)
a(t) = a(dec) if (λ / d(t)) * (u(t – Λ) – v(t – Λ)) < a(dec)
a(t) = (λ / d(t)) * (u(t – Λ) – v(t – Λ)) else

It probably looks simpler using an if-statement:

a(t) = (λ / d(t)) * (u(t – Λ) – v(t – Λ))

IF a(t) > a(acc) THEN
a(t) = a(acc)
ELSEIF a(t) < a(dec) THEN
a(t) = a(dec)
END IF

This model already catches a lot of nuances of car traffic. I hope I was able to give you some  insight into what car-following models are and how you can fine-tune them to satisfy certain conditions.